The exact electric field at point
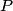 is is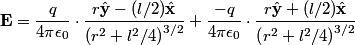 where the first term is from the positive charge and the second term is from the the negative charge. The y-components of the electric fields due to the two charges cancel, so 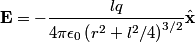 When  is much greater than is much greater than 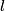 , , 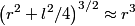 , so , so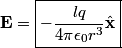 Thus, answer (E) is correct. |